How To Check If Data Is Normally Distributed In R

Many of the statistical methods including correlation, regression, t tests, and analysis of variance assume that the data follows a normal distribution or a Gaussian distribution. These tests are chosen parametric tests, because their validity depends on the distribution of the data.

Normality and the other assumptions fabricated by these tests should be taken seriously to draw reliable interpretation and conclusions of the enquiry.

With big enough sample sizes (> 30 or 40), there'due south a pretty good gamble that the information will be unremarkably distributed; or at least close plenty to normal that you can get abroad with using parametric tests, such every bit t-examination (central limit theorem).

In this chapter, you volition larn how to check the normality of the data in R by visual inspection (QQ plots and density distributions) and by significance tests (Shapiro-Wilk exam).

Contents:

Prerequisites
Demo data
Examples of distribution shapes
Bank check normality in R
- Visual methods
- Shapiro-Wilk'south normality test
Summary
References

Related Book

Practical Statistics in R II - Comparing Groups: Numerical Variables

Prerequisites

Make sure you have installed the post-obit R packages:

tidyverse for data manipulation and visualization
ggpubr for creating easily publication fix plots
rstatix provides piping-friendly R functions for easy statistical analyses

Start by loading the packages:

            library(tidyverse) library(ggpubr) library(rstatix)

Demo information

We'll utilise the ToothGrowth dataset. Inspect the data by displaying some random rows past groups:

            set.seed(1234) ToothGrowth %>% sample_n_by(supp, dose, size = 1)

            ## # A tibble: 6 x 3 ##     len supp   dose ##   <dbl> <fct> <dbl> ## 1  21.5 OJ      0.5 ## 2  25.8 OJ      ane   ## 3  26.4 OJ      2   ## iv  11.2 VC      0.five ## 5  eighteen.8 VC      1   ## vi  26.7 VC      two

Examples of distribution shapes

Normal distribution

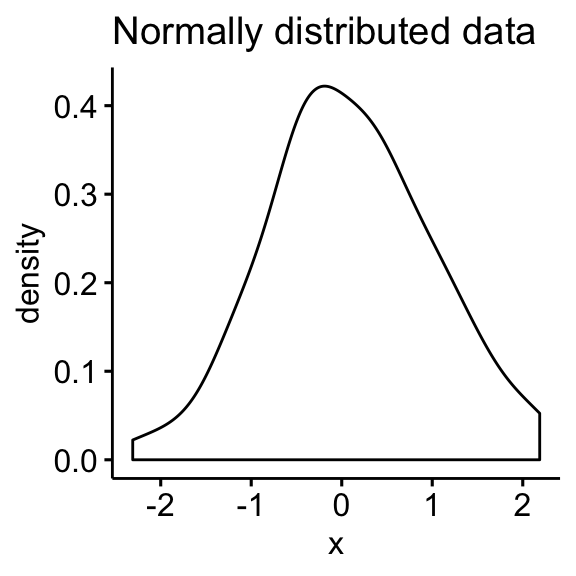
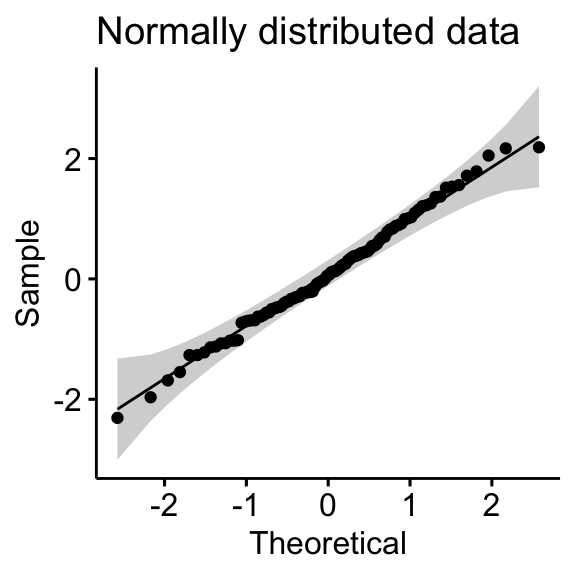
Skewed distributions

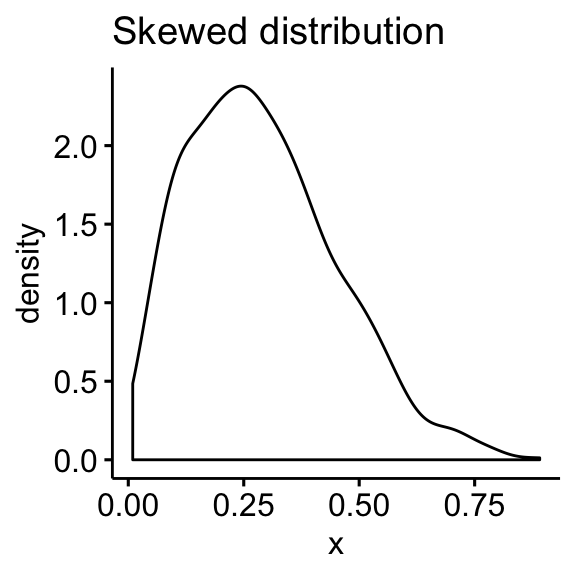
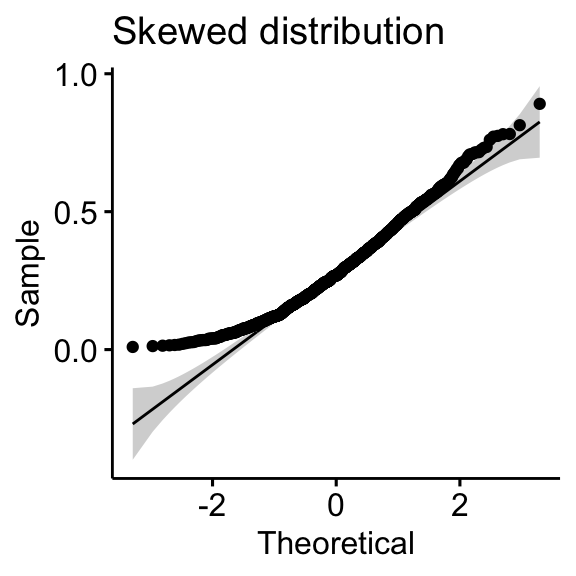
Check normality in R

Question: Nosotros want to test if the variable len (molar length) is normally distributed.

Visual methods

Density plot and Q-Q plot can be used to check normality visually.

Density plot: the density plot provides a visual judgment near whether the distribution is bell shaped.
QQ plot: QQ plot (or quantile-quantile plot) draws the correlation betwixt a given sample and the normal distribution. A 45-degree reference line is also plotted. In a QQ plot, each observation is plotted as a single dot. If the data are normal, the dots should form a straight line.

              library("ggpubr") # Density plot ggdensity(ToothGrowth$len, fill = "lightgray") # QQ plot ggqqplot(ToothGrowth$len)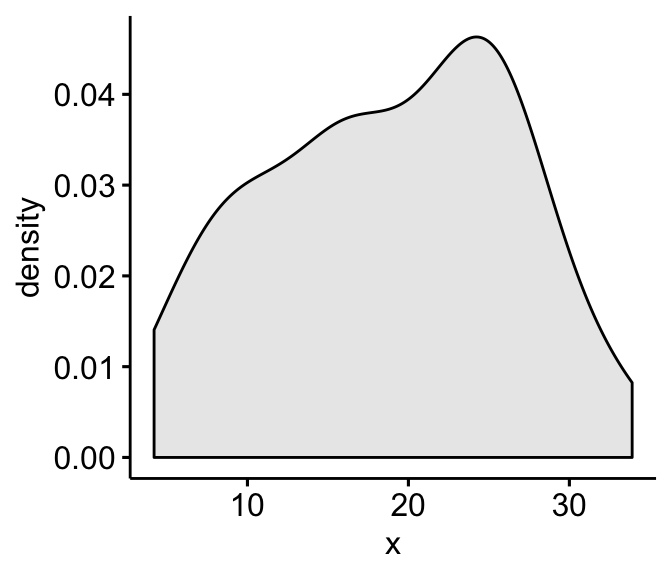

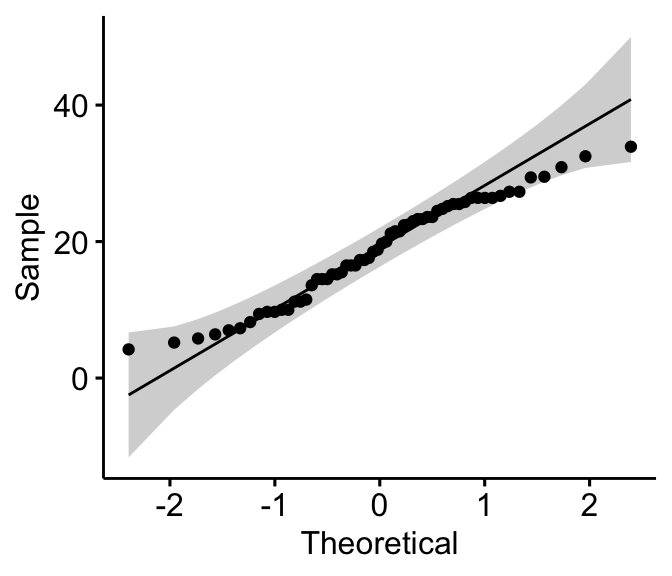
As all the points fall approximately along this reference line, we can assume normality.

Shapiro-Wilk's normality examination

Visual inspection, described in the previous section, is ordinarily unreliable. It's possible to use a significance examination comparing the sample distribution to a normal ane in order to define whether data bear witness or not a serious deviation from normality.

In that location are several methods for evaluate normality, including the Kolmogorov-Smirnov (Thou-S) normality test and the Shapiro-Wilk's test.

The nil hypothesis of these tests is that "sample distribution is normal". If the examination is significant, the distribution is non-normal.

Shapiro-Wilk's method is widely recommended for normality exam and it provides better ability than K-S. It is based on the correlation between the data and the corresponding normal scores (Ghasemi and Zahediasl 2012).

Note that, normality test is sensitive to sample size. Small samples almost often pass normality tests. Therefore, it's important to combine visual inspection and significance test in society to take the right decision.

The R function shapiro_test() [rstatix parcel] provides a pipe-friendly framework to compute Shapiro-Wilk test for one or multiple variables. It also supports a grouped data. Information technology's a wrapper effectually R base of operations function shapiro.test().

Shapiro test for 1 variable:

              ToothGrowth %>% shapiro_test(len)

              ## # A tibble: i x 3 ##   variable statistic     p ##   <chr>        <dbl> <dbl> ## ane len          0.967 0.109

From the output to a higher place, the p-value > 0.05 implying that the distribution of the data are not significantly dissimilar from normal distribution. In other words, we can assume the normality.

Shapiro test for grouped data:

              ToothGrowth %>%   group_by(dose) %>%   shapiro_test(len)

              ## # A tibble: iii x 4 ##    dose variable statistic     p ##   <dbl> <chr>        <dbl> <dbl> ## one   0.5 len          0.941 0.247 ## 2   1   len          0.931 0.164 ## 3   2   len          0.978 0.902

Shapiro examination for multiple variables:

              iris %>% shapiro_test(Sepal.Length, Petal.Width)

              ## # A tibble: ii x iii ##   variable     statistic            p ##   <chr>            <dbl>        <dbl> ## 1 Petal.Width      0.902 0.0000000168 ## 2 Sepal.Length     0.976 0.0102

Summary

This chapter describes how to check the normality of a data using QQ-plot and Shapiro-Wilk test.

Note that, if your sample size is greater than 50, the normal QQ plot is preferred considering at larger sample sizes the Shapiro-Wilk exam becomes very sensitive even to a minor divergence from normality.

Consequently, we should not rely on only ane arroyo for assessing the normality. A amend strategy is to combine visual inspection and statistical test.

References

Ghasemi, Asghar, and Saleh Zahediasl. 2012. "Normality Tests for Statistical Analysis: A Guide for Not-Statisticians." Int J Endocrinol Metab 10 (two): 486–89. doi:10.5812/ijem.3505.